| |
|||||||||
| |
|
|
|
|
|
|
|
||
| Home | About | Literature | Site Map | MSDS | Contact | Engineers | Shows | Links | Samples | RFQ | Catalog Numbers |

Tension estimates when pulling heavy electrical or telephone cable into conduit have been reasonably accurate using the equations in American Polywater's Pull-Planner™ 3000 Software. However, the tension in outside plant fiber optic pulls has not been so easy to predict. Fiber optic cable pullers have learned that both the type of duct and the method used to place the duct affect the tension in a fiber optic cable pull.
Experienced cable pullers know it is not possible to pull fiber substantial distances in innerduct dropped and buried in an open trench. The undulations in the conduit from reel memory introduce too much bend.
Studies conducted by Bell Labs showed much lower tensions were needed to pull fiber optic cable into plow-buried 2" innerduct than into 1.25" innerduct buried with the same plow.¹ The stiffer walled, larger innerduct simply plowed "straighter" than the smaller.
These differences are due to the "duct factor" in continuous reeled type innerduct. Duct factor can be thought of as a measure of how close the placed duct is to a true straight line. It is this duct factor variable that has limited the use of the traditional cable pulling equations to predict tension in fiber optic pulls. Can we quantify the duct factor to get better tension estimates when pulling fiber optic cable into innerduct?
A Duct Displacement Model
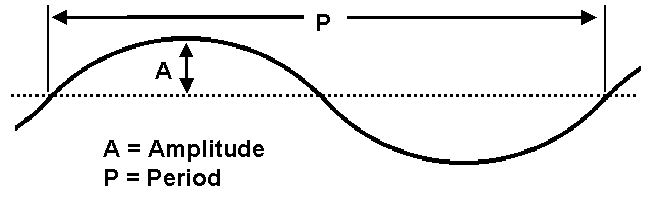
We can determine the amount of bend in an innerduct with a regular displacement by modeling it as shown at right. Here the regular conduit displacement is treated as a two-dimensional wave with a defined height (amplitude) and length (period).
Using this approach, we determine geometrically how much bend (in degrees per unit of length) is in the duct. The following table presents some calculations from this model.
| Amplitude | Period | Bend | |||
|---|---|---|---|---|---|
| 0 in | 0 mm | 30 ft | 9 M | 0°/ft | 0°/M |
| 0.5 in | 13 mm | 30 ft | 9 M | 0.085°/ft | 0.279°/M |
| 1 in | 25 mm | 30 ft | 9 M | 0.170°/ft | 0.558°/M |
| 2 in | 51 mm | 30 ft | 9 M | 0.339°/ft | 1.11°/M |
| 6 in | 153 mm | 30 ft | 9 M | 0.678°/ft | 2.22°/M |
| 2 in | 51 mm | 20 ft | 6 M | 0.763°/ft | 2.50°/M |
| 2 in | 51 mm | 10 ft | 3 M | 3.04°/ft | 9.97°/M |
Appropriate amplitudes and periods depend on field specifics. The period generally results from innerduct memory and reel diameter, and numbers in the range of 15 to 45 feet (5 to 15 M) seem typical (remember this is actually two displacements as the drawing shows).
The amplitude depends on the physical restraint containing the duct and the force straightening the duct during installation. For innerduct dropped in a trench, the amplitude could be 6 inches (150 mm) or more per period. For innerduct in a 4-inch (100-mm) conduit, the amplitude is probably less than 1 inch (25 mm).
The table shows that with zero (0) amplitude, there is no bend in the conduit, as we expect. At typical displacements, the hidden bend can run from a few hundredths of a degree per foot (or meter) to 3 degrees/ft (10 degrees/M) or higher.
A displacement of ± 1 inch (25 mm) every 30 feet (9 M) is hardly noticeable in laid out duct. While the calculated bend of 0.17 degrees/ft (0.558 degrees/M) does not seem like a lot, it is 170 degrees per thousand feet (558 degrees per KM) of pull. To understand what these levels of bend mean, we need to extend this model into tension calculations.
Tension Calculations Using the Model
The bend calculated from the model is combined with friction data on Polywater® Lubricants (bends versus straight sections) to determine the duct factor. The higher the duct factor, the higher the pulling tension compared to pulling in a truly straight duct, which has a duct factor of zero (0).
The table below shows the duct factor, the calculated tension for a 2500-foot (760 M) pull using the duct factor and the total bend in the pull. The amplitudes and periods are the ones used previously.
| A (in/mm) | P (ft/M) | Duct Factor | Tenison in 2500 ft (760M) | Total Bend | |||
|---|---|---|---|---|---|---|---|
| 0 | 0 | 30 | 9 | 0 | 56 lbs | 250 N | 0° |
| 0.5 | 13 | 30 | 9 | 0.89 | 137 lbs | 610 N | 212° |
| 1 | 25 | 30 | 9 | 1.78 | 231 lbs | 1.02 kN | 424° |
| 2 | 51 | 30 | 9 | 3.55 | 1076 lbs | 4.78 kN | 848° |
| 6 | 153 | 30 | 9 | 6.78 | 30400 lbs | 135 kN | 1694° |
| 2 | 51 | 20 | 6 | 7.47 | 63600 lbs | 282 kN | 1908° |
| 2 | 51 | 10 | 3 | 15.93 | >10 ^ 9 lbs | 10 ^ 6 kN | 7606° |
The projected pulling tension is 56 lbs (250 N) at zero amplitude (zero duct factor). We see that small, but regular duct displacements can produce from hundreds to tens of thousands of pounds (Newtons) of add-on tension, tension caused by the hundreds of degrees of "hidden" bend.
The cable data used in the table above is typical, and the friction coefficient represents the best lubricant in the business, our own Polywater® F. We can see from the data that it would be very difficult to make long fiber pulls into innerduct with a duct factor above 3, and duct factors less than 1 are the most desirable.
Implications of the Model
This model indicates that cable pulling tensions into so-called "straight" innerduct sections (non-zero duct factor) are non-linear. That is, you can't pull twice as far with twice the tension. The table shows a duct factor of 1.78 and a 2500-foot pull tension of 231 lbs (1.02 kN) for a displacement amplitude of 1-inch (25 mm) and a period of thirty feet (9 M). For a 5000-foot pull (1340 M) into the same duct, the model predicts almost ten times as much tension (2150 lbs/9.55 kN), well above the maximum for most fiber optic cable. In fact, the model predicts you can only pull 3550 feet (1080 M) into this duct with tension less than 600 lbs (2.65 kN).
The model also shows the importance of the coefficient of friction. In the previous example, the projected tension on the 2500-foot pull goes up by a factor of more than 3 (from 231 to 1027 lbs) (1.02 to 4.56 kN) when the friction coefficient is raised from .015 to 0.25. The low friction produced by Polywater® F is very important when pulling into continuous innerduct.
Using Field Data to Determine Duct Factor
So far, innerduct displacements have been used to theoretically determine a duct factor. The duct factor can also be determined from measured tension in field pulls. This duct factor can be used to compare installation methods or to improve tension prediction for additional pulls into the same duct.
Let's demonstrate this with some data from reference 1. In the following table the tension was measured in the Bell Labs' fiber pulls. The duct factors have been determined from this measured tension.
| Duct Type | Measured Tension | Duct Factor | |
|---|---|---|---|
| 1.5" corrugated (38 mm) | 444 lbs | 1.97 kN | 4.11 |
| 2" corrugated (51 mm) | 423 lbs | 1.88 kN | 4.04 |
| 1.25" smoothwall (32 mm) | 331 lbs | 1.47 kN | 3.64 |
| 1.5" smoothwall (38 mm) | 104 lbs | 461 N | 1.38 |
| 2" smoothwall (51 mm) | 73 lbs | 324 N | <0.3 |
Only the larger smoothwall ducts had a duct factor less than 3 in this plowing test. The tension of 73 lbs (324 N) in the plowed 2" (51 mm) smoothwall compares very favorably with the theoretical absolute straight tension of 41 lbs (182 N) with a zero duct factor.
The duct factor can be used to calculate maximum pulling distances of 4200 feet (1280 M) and 6000 plus feet (1830 M) through the 1.5" and 2" (38 and 51 mm) smoothwall respectively. While 4000-foot (1220 M) pulls are practical through properly plowed ducts, pulls of over 6000 feet (1830 M) are not common. The extrapolations from the model may be slightly high. Only doing longer pulls would tell for sure.
Duct Factor Calculator Put on Web
If you are interested in working some of your own examples, a Duct Factor and Tension Calculator is available on American Polywater's web page. The calculator will determine a duct factor and pulling tension from the input you provide (amplitude, period, cable weight, length of pull, incoming tension, and friction coefficient). While the web calculator is not set up to calculate a duct factor from field tensions, it is relatively easy to do this using trial and error input.
Summary
A model is used to determine the pulling tension effects of small but regular innerduct displacements. The model develops a duct factor, which is then used in pulling tension calculations.
The model is only useful for lightweight cable pulled into continuous innerduct with a regular displacement. Though not proven, the model does give much better agreement with "typical" fiber optic pulling tensions than do traditional pulling calculations.
In the next issue of TeleTopics, data from test pulls into continuous duct with controlled displacement will be compared with projections from the model. The editor welcomes any input or field experiences in this area.
View this article in PDF Format
Use this free Calculator to determine duct factor in fiber optic cable pulling
View a 12-minute training video on Fiber Optic Cable Pulling & Lubrication
For Subscriptions, Comments, or Questions contact: tteditor@polywater.com
Home |
About |
Site Map |
Literature |
Samples |
Links |
Reps |
Videos |
Pumps |
RFQ
Codes |
Engineering |
Shows |
Spotlight |
Newsletters |
MSDS |
Translations |
Contacts |
Jobs

11222 60th ST N | Stillwater, MN 55082-9310 USA
1-(651) 430-2270 (Voice) | 1-(651) 430-3634 (Fax)
1-(800) 328-9384 (Toll-Free US/Canada Only)
Copyright © 2001 - 2015 American Polywater Corporation | ![]() 6/5/15
6/5/15